
The perpendicular bisector of a chord \(AB\) of a circle intersects it at \(P\) and \(Q\). Demonstrate that \(arc \ PEA\) is equal to \(arc\ PFB\).
Proof:
Let \(PQ\) be the perpendicular bisector of \(AB\), which intersects it at \(M\) and always passes through the centre of the circle \(O\).
Now, Join \(AP\) and \(BP\).
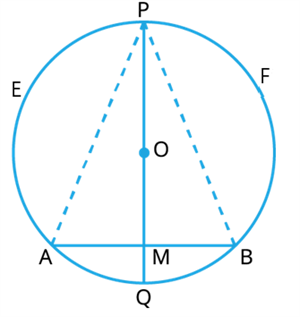
In \(△ APM\) and \(△ BPM\),
\(AM =\) ()
\(∠PMA=∠PMB=\)\(^°\)
\(PM = \) ()
Thus, \(△APM≅△BPM\) []
Therefore, \(PA =\)
If two chords (\(PA = PB\)) are equal, then the corresponding arcs are congruent.
That is, \(arc\) \(PEA ≅ arc\) \(PFB\).