
If a straight line intersects two circles having the same centre \(O\) at \(A\),\(B\),\(C\), and \(D\). Prove that \(AB\) equals \(CD\)
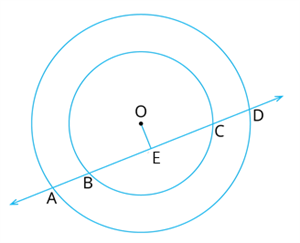
Explanation:
Draw \(OE ⊥ AD\),
In bigger circle is chord
\(OE ⊥ AD\).
Therefore, \(AE=\)
[] --------(1)
In the smaller circle, is chord
\(OE ⊥ BC\)
\(BE=\)
[] ------(2)
subtracting (1) and (2),
\(AE-BE=ED-EC\)
\(AB=\)