1. Determine the given question using appropriate Euclid’s axiom : In the Figure, we have \(X\) and \(Y\) are the mid-points of \(AB\) and \(CB\) and\(AX= CY\). Prove that \( AB= CB\).
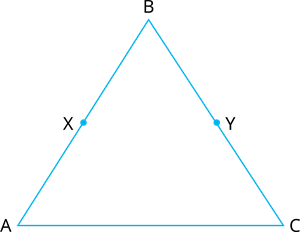
\(2AX = \)
\(2CY = \)
According to Euclid axiom, 'things which are double of things are equal to one another'.
2. In the Figure, we have \( BX= \frac{1}{2} AB\), \( BY= \frac{1}{2} CB\) and \( AB=CB \). Prove that\( BX= BY\).

\(2\)BX\(= 2\)
Hence, BX \(=\)
Euclid's axiom: Things which are double of things are to one another