1. In the Diagram. , if \(∠k = ∠m\), \(∠l = ∠n\) and \(∠ m= ∠n\), write the relation between \(∠k\) and \(∠l\), using an Euclid’s axiom.
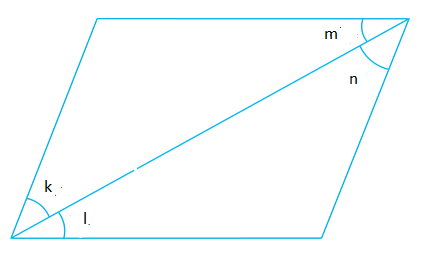
Euclid’s first axiom says, the things which are to equal thing are equal to one another.
2. In Daigram. we have : \(AC = PR\), \(C\) is the mid-point of \(AB\) and \(R\) is the mid-point of \(PQ\). Using an Euclid’s axiom, show that \( AB= PQ\).
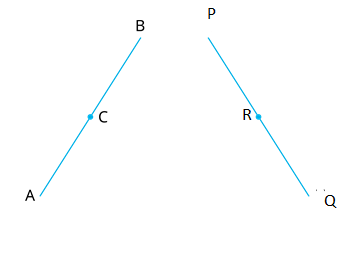
\( AB=\) \(2\) as is the mid-point of \(AB\)
\( PQ=\) \(2\) as is the mid-point of \(PQ\)
\(AB = PQ\), because things which are double of the same things are to one another.