In Fig., \(BA || ED\) and \(BC || EF\). Show that \(∠ ABC + ∠ DEF = 180^°\)
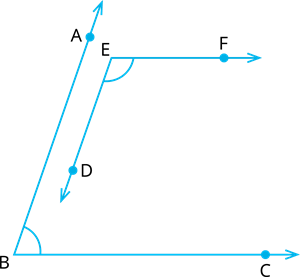
Proof:
Produce \(ED\) to meet \(BC\) at point \(P\).
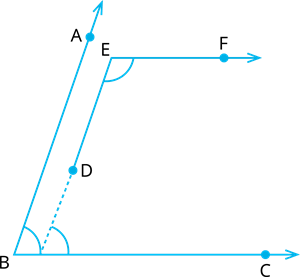
Now, \(EF∥BC\) and \(EP\) is the transversal.
The sum of co-interior angles on the same side of the transversal is \(^°\).
Therefore, \(∠DEF+∠EPC=\)\(^°\) ------(1)
Again, \(EP∥AB\) and \(BC\) is transversal.
Therefore, \(∠EPC=∠\) ---------(2) [Corresponding angles]
From (1) and (2), We get the result.