If in Fig., bisectors \(AP\) and \(BQ\) of the alternate interior angles are parallel, then show that \(l || m\).
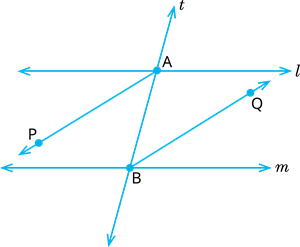
Proof:
Since, \(AP|| BQ\) and \(t\) is transversal
Therefore \(∠PAB = ∠\) [alternate interior angles]
\(2 ∠PAB = 2 \)

So, alternate interior angles are equal.
We know that,
Hence, we get the result.