In Fig., \(∠ PQR = ∠ PRQ\), then prove that \(∠ PQS = ∠ PRT\).
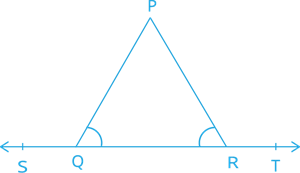
Proof:
Taking \(ST\) is a straight line, so the sum of all angles made on it is \(^°\)
That is, \(∠PQS + ∠PQR =\)\(^°\) -----(1)
Also, \(∠PRQ + ∠PRT =\)\(^°\) ----(2)
By equating both the equations because RHS of both the equation is equal
So, \(∠PQS + ∠PQR = ∠PRQ + ∠PRT\)
Since, \(∠PQR = ∠\)
\(∠PQS = ∠PRT\)
Hence Proved.