If two lines intersect, prove that the vertically opposite angles are equal.
Proof:
Let the two lines \(AB\) and \(CD\) intersect at point \(O\).
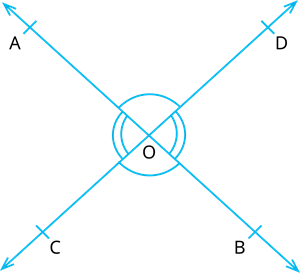
To prove: The vertically opposite angles are equal
That is, we need to prove the following
(i) \(∠AOC=∠\)
(ii) \(∠AOD=∠\)
Explanation:
(i) Since, ray \(OA\) stands on line \(CD\)
Therefore, \(∠AOC+∠AOD=\) \(^°\) [Linear pair axiom] ------(1)
Similarly, ray \(OD\) stands line \(AB\).
Therefore, \(∠AOD+∠BOD=\)\(^°\) ------(2)
From (1) and (2),
\(∠AOC+∠AOD=∠AOD+∠BOD\)
\(∠AOC=\)
(ii) Now, ray \(OD\) stands on line \(AB\).
Therefore, \(∠AOD+∠BOD=\)\(^°\) -------(3)
Similarly, ray \(OB\) stands on line \(CD\).
Therefore, \(∠DOB+∠BOC=\)\(^°\) -------(4)
From (3) and (4),
\(∠AOD+∠BOD=∠DOB+∠BOC\)
\(∠AOD=∠\).