In the given figure, \(POQ\) is a line. Ray \(OR\) is perpendicular to line \(PQ\). \(OS\) is another ray lying between rays \(OP\) and \(OR\). Prove that \(∠ROS = (\frac{1}{2}) (∠QOS – ∠POS)\)?
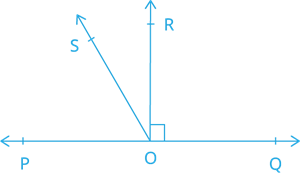
Proof:
\(POQ\) is a straight line.
So, the sum of all angles made on it is \(^°\)
\(∠POS + ∠ROS + ∠ROQ =\) \(^°\)
Since \(∠ROQ =\)\(^°\), \(∠POS + ∠ROS +\)\( =\)\(^°\)
\(∠POS + ∠ROS =\)\(^°\)
\(∠ROS =\)\(^° – ∠POS\) ---(2)
From figure, \(∠ROS + ∠ROQ = ∠\)
That is, \(∠ROS +\)\(^° = ∠QOS\)
\(∠ROS = ∠QOS –\)\(^°\) –---(2)
Now Adding both the equations (1) and (2) we get,
\(∠ROS + ∠ROS =\)\(^° – ∠POS + ∠QOS –\)\(^°\)
\(2∠ROS =(∠QOS – ∠POS)\)
\(∠ROS = \frac{1}{2}(∠QOS – ∠POS)\)
Hence Verified.