Bisectors of interior \(∠B\) and exterior \(∠ACD\) of a \(△ ABC\) intersect at the point \(T\). Prove that \(∠BTC=\frac{1}{2}∠BAC\) .
Proof:
For a triangle \(△ ABC\), produce \(BC\) to \(D\) and the bisectors of \(∠ABC\) and \(∠ACD\) meet at point \(T\).
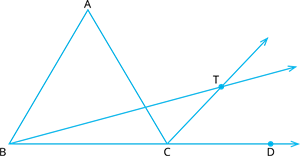
Now, \(CT\) is a bisector of \(∠ACD\)
Therefore, \(\frac{1}{2} ∠ACD=∠\) ------(a)
Also, \(BT\) is a bisector of \(△ABC\)
Therefore, \(∠CBT=\frac{1}{2}∠\) ----- (b)
In \(△ ABC\), \(∠ACD\) is an exterior angle.
Therefore, \(∠ACD=∠ABC+∠ \)
\(\frac{1}{2} ∠ACD=\frac{1}{2} ∠\)\(+\frac{1}{2} ∠ABC\)
\(∠TCD=\frac{1}{2} ∠\)\(+\frac{1}{2} ∠ABC\) ------(1)
Again, in \(△ BTC\),
\(∠TCD=∠BTC+∠\) (since, Exterior angle \(=\) sum of two opposite angles)
\(∠TCD=∠BTC+\frac{1}{2}∠\) ------(2) [From equation (b)]
From (1) and (2),
\(\frac{1}{2} ∠\)\(+\frac{1}{2} ∠ABC=∠BTC+\frac{1}{2}∠\)
\(\frac{1}{2}∠CAB=∠BTC\)
That is, \(\frac{1}{2}∠BAC=∠BTC\).