In Fig., \(∠1 = \)58\(^°\) and \(∠6 = \)122\(^°\). Show that the lines \(m\) and \(n\) are parallel.
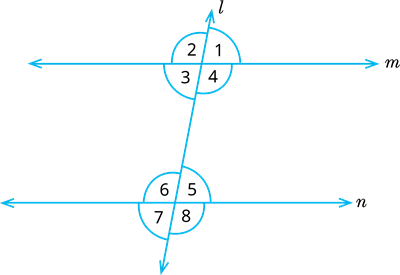
Proof:
Given that, \(∠1 = \)58\(^°\) and \(∠6 = \)122\(^°\)
Here, \(∠1 = ∠\) [vertically opposite angles]
\(∠\)\( = ∠1 = \)58\(^°\)
Now, \(∠3 + ∠6 =\) \(^°\)
We know that, if the sum of two interior angles on same side of \(l\) is \(^°\), then lines are parallel.
Hence, \(m || n\).