In Fig.,\(m\) and \(n\) are two plane mirrors perpendicular to one another. Prove that incident ray \(JH\) is parallel to reflected ray \(IK\).
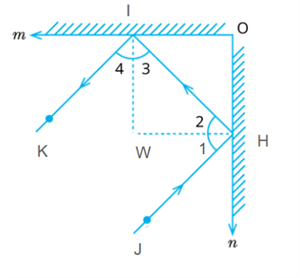
Proof:
Let normals at \(H\) and \(I\) meet at \(W\).
As mirrors are perpendicular to each other
Therefore, \(IW\)\( || \) and \(HW\)\( || \) .
So, \(IW\)\( ⊥ \)\(WH\),
That is, \(∠ \)\(IWH\)\( = 90^°\)
Therefore, \(∠ 3 + ∠ 2 =\)\(^°\) (Angle sum property) ------(1)
Also, \(∠1 = ∠2\) and \(∠4 = ∠3\) (Angle of incidence \(=\) Angle of reflection)
Thus, \(∠1 + ∠4 =\)\(^°\)-----(2)
Adding (1) and (2),
we have \(∠1 + ∠2 + ∠3 + ∠4 =\)\(^°\)
That is, \(∠\)\(JHI\)\( + ∠\) \(KIH\)\(=\)\(^°\)
Hence, \(JH\)\(|| \)\(IK\)