
\(PS\) is a median of \(\bigtriangleup PQR\), and \(T\) is its midpoint. The line through \(Q\) and \(T\) intersects \(PR\) at \(U\), prove that the segment \(PU\) is one-third of \(PR\).
Solution:
Given:
In \(△ PQR\), \(PS\) is a median and \(T\) is the mid-point of \(PS\).
Now, Draw \(SV || TU\) as shown in below figure.
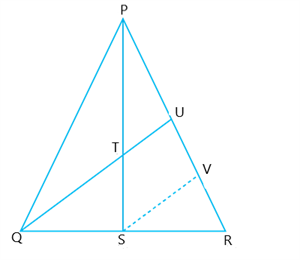
In \(△ PSV\), \(T\) is the mid-point of \(PS\) and \(TU || SV\).
Thus, by converse of mid-point theorem, 'The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.'
\(U\) is mid-point of \(PV\).
\(PU=\) --------\((1)\)
In \(△ UQR\),
\(S\) is mid-point of \(QR\) and \(SV || QU\).
So, again by converse of mid-point theorem, 'The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.'
is mid-point of \(UR\).
\(UV=\) ---------\((2)\)
From \((1)\) and \((2)\)
Thus, \(PU = UV = VR\).
\(PR=PU+UV+VR\)
\(PR=3\)
That is, \(PU=\frac{1}{3}PR\)
Hence, proved.