
If \(W\), \(X\), \(Y\), and \(Z\) are the mid-points of the sides of rectangle \(ABCD\). Verify that the quadrilateral \(WXYZ\) formed by joining them is a rhombus.
Construction : Join \(A\) and \(C\)
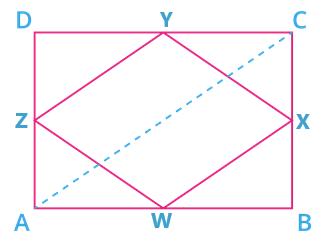
Proof : Since \(ABCD\) is a rectangle, \(AD = BC\)
\(\Rightarrow \frac{1}{2}AD = \frac{1}{2}\)
\(\Rightarrow AZ = BX\) and \(DZ = CX\) - - - - - (I)
In \(\Delta ABC\), is the mid-point of \(AB\) and is the mid-point of \(BC\).
By the mid-point theorem 'The line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.'
\(\Rightarrow WX\ || \ AC\) and \(WX = \frac{1}{2}\) - - - - (II)
Similarly, in \(\Delta ADC\), is the mid-point of \(CD\) and is the mid-point of \(AD\).
By the mid-point theorem,'The line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.'
\(\Rightarrow YZ \ || \ AC\) and \(YZ= \frac{1}{2}\) - - - - (III)
From (I) and (II), we get, \(WX \ || \ YZ\).
Thus, \(WXYZ\) is a parallelogram.
In \(\Delta ZAW\) and \(\Delta XBW\):
\(AW = \) [Given]
\(\angle ZAW = \angle \) [Each \(90^\circ\)]
\(AZ = BX\) [Using (I)]
Thus, \(\Delta ZAW \cong \Delta XPW\) [by ].
\(\Rightarrow WZ = WX\) [by CPCT]
But, we know that opposite sides of parallelogram are equal.
\(WX = YZ\) and \(WZ = YX\)
So, \(WX = YX = YZ = WZ\).
Hence, \(WXYZ\) is a rhombus.
\(\Rightarrow \frac{1}{2}AD = \frac{1}{2}\)
\(\Rightarrow AZ = BX\) and \(DZ = CX\) - - - - - (I)
In \(\Delta ABC\), is the mid-point of \(AB\) and is the mid-point of \(BC\).
By the mid-point theorem 'The line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.'
\(\Rightarrow WX\ || \ AC\) and \(WX = \frac{1}{2}\) - - - - (II)
Similarly, in \(\Delta ADC\), is the mid-point of \(CD\) and is the mid-point of \(AD\).
By the mid-point theorem,'The line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.'
\(\Rightarrow YZ \ || \ AC\) and \(YZ= \frac{1}{2}\) - - - - (III)
From (I) and (II), we get, \(WX \ || \ YZ\).
Thus, \(WXYZ\) is a parallelogram.
In \(\Delta ZAW\) and \(\Delta XBW\):
\(AW = \) [Given]
\(\angle ZAW = \angle \) [Each \(90^\circ\)]
\(AZ = BX\) [Using (I)]
Thus, \(\Delta ZAW \cong \Delta XPW\) [by ].
\(\Rightarrow WZ = WX\) [by CPCT]
But, we know that opposite sides of parallelogram are equal.
\(WX = YZ\) and \(WZ = YX\)
So, \(WX = YX = YZ = WZ\).
Hence, \(WXYZ\) is a rhombus.