
In a trapezium \(ABCD\), points \(E\) and \(F\) are the mid points of sides \(AD\) and \(BC\). Verify that \(EF\) is parallel to \(AB\) and \(CD\), and that its length is half the sum of the lengths of \(AB\) and \(CD\).
Proof:
Now, join \(BE\) and extend it to meet \(CD\) produced at \(G\) such that \(BD\) and \(EF\) will intersect at \(O\).
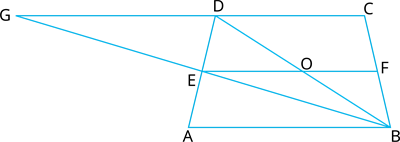
In \(△ GCB\),
\(E\) and \(F\) are the mid-points of \(BG\) and \(BC\) respectively.
Then by mid-point theorem,
\(EF∥\)
But \(GC∥AB\) or \(CD∥AB\) [given]
Therefore, \(EF∥AB\)
In \(△ ADB\),
\(AB∥EO\) and \(E\) is the mid-point of \(AD\).
Hence, by converse of mid-point theorem, \(O\) is mid-point of \(BD\).
Also, \(EO=\frac{1}{2}\) [] .....(1)
In \(△ BDC\),
\(OF ||\) and \(O\) is the mid-point of \(BD\).
Therefore, \(OF=\frac{1}{2}\) [] ......(2)
Now, adding (1) and (2) we get,
\(EO+OF=\frac{1}{2}AB+\frac{1}{2}CD\)
That is, \(EF=\frac{1}{2}(AB+CD)\)
Hence, proved.