
\(MNOP\) is a rectangle in which diagonal \(MO\) bisects \(∠M\) as well as \(∠O\). Confirm that:
(i) \(MNOP\) is a square
Proof:
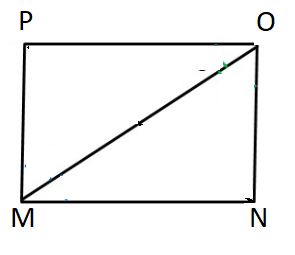
Given that \(MNOP\) be a rectangle such that \(MO\) bisects \(∠M\) as well as \(∠O\),
So \(∠NMO= ∠PMO\) and, \(∠POM = ∠\) -----(1)
As we know that every rectangle is a parallelogram.
\(MNOP\) is a parallelogram.
\(∠NOM = ∠\) -----(2) [ Alternate interior angles are equal]
From (1) and (2), we have
\(∠POM = ∠\) -----(3)
In \(∆MNO\),
\(∠POM = ∠PMO\) then, \(OP = \) [Sides opposite to equal angles of a triangle are equal]
Similarly, \(MN = \)
So, \(MNOP\) is a rectangle having adjacent sides equal.
\(MNOP\) is a square.
Hence, proved.
(ii) diagonal \(NP\) bisects \(∠N\) as well as \(∠P\).
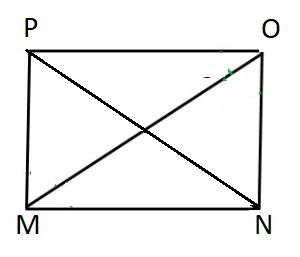
Proof:
Since, \(MNOP\) is a square
\(MN = NO = OP = PM\)
So, In \(∆MNP\), as \(MN = \)
\(∠MNP = ∠\) [Angles opposite to equal sides of a triangle are equal] -----.(1)
Similarly, \(∠ONP = ∠\) ------(2)
\(∠ONP = ∠\) [Alternate interior angles are equal] -----(3)
From (1) and (3)
\(∠ONP = ∠MNP\)
From (2) and (3)
\(∠MPN = ∠\)
So, \(NP\) bisects \(∠N\) as well as \(∠P\).
Hence, proved.