
Let \(P\) is the mid-point of the side \(CD\) of a parallelogram \(ABCD\). The line drawn through \(C\) parallel to \(PA\) meets \(AB\) at \(Q\) and the extension of \(DA\) at \(T\). Demonstrate that \(DA = AT\) and \(CQ = QT\).
Proof:
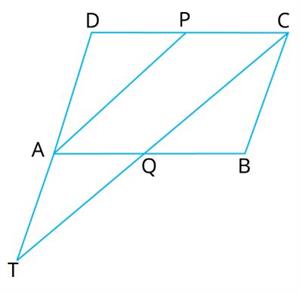
\(ABCD\) is a parallelogram.
Therefore, \(BC=AD\) and \(BC∥AD\)
Also, \(DC=AB\) and \(DC∥AB\)
As, \(P\) is the mid-point of \(DC\).
Then, \(DP=PC=\frac{1}{2}DC\)
Now, \(QC∥AP\) and \(PC∥AQ\).
Thus, \(APCQ\) is a parallelogram.
Therefore, \(AQ=PC=\frac{1}{2}DC=\frac{1}{2}AB=\) [∵DC=AB] .....(1)
Now, in \(△AQT\) and \(△BQC\), \(AQ=\) [From (1)]
\(∠AQT=∠\) [vertically opposite angles] and
\(∠ATQ=∠\) [alternate interior angles]
Therefore, \(△AQT≅△\) [AAS congruence rule]
Then, \(AR = BC\) [by rule]
But \(BC = \)
Therefore, \(AT = DA\) and \(CQ = QT\) [CPCT rule]
Hence, proved.