
If the angle bisectors of \(∠A\) and \(∠B\) of a quadrilateral \(ABCD\) meet at \(P\), those of \(∠B\) and \(∠C\) at \(Q\), those of \(∠C\) and \(∠D\) at \(T\) and of \(∠D\) and \(∠A\) at \(S\). Demonstrate that the quadrilateral formed by these points is a quadrilateral.
Explanation:
Given that \(ABCD\) is a quadrilateral and all angles bisectors from a quadrilateral \(PQTS\).
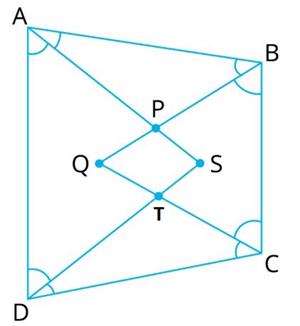
The sum of all angles in a quadrilateral is \(360^°\).
Therefore, \(∠A+∠B+∠C+∠D=360^°\)
\(\frac{1}{2}(∠A+∠B+∠C+∠D)=\)\(^°\)
\(∠PAB+∠PBA+∠TCD+∠TDC=\)\(^°\) .....(1)
In \(△ APB\), by angle sum property,
\(∠PAB+∠ABP+∠BPA=180^°\)
\(∠PAB−∠ABP=180^°−∠BPA\) .....(2)
Similarly, In \(△ TDC\),
\(∠TDC+∠DCT+∠CTD=180^°\)
\(∠TDC+∠DCT=180^°−∠CTD\) .....(3)
Substituting (2) and (3) in (1),
\(180^°−∠BPA+180^°−∠DTC=180^°\)
\(∠BPA+∠DTC=180^°\)
\(=180^°\) [\(∠BPA=∠SPQ\) and \(∠DTC=∠STQ\) are vertically opposite angles]
Therefore, \(PQTS\) is a quadrilateral.