
Two parallel lines \(l\) and \(m\) are intersected by a transversal \(p\) (see figure). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
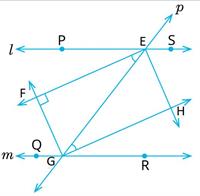
It is given that \(PS || QR\) and transversal \(P\) intersects them at points \(E\) and \(G\) respectively.
The bisectors of \(∠ PEG\) and \(∠ EGQ\) intersect at \(F\) and bisectors of \(∠ EGR\) and \(∠ SEG\) intersect at \(H\).
We are to show that quadrilateral \(EFGH\) is a rectangle.
Now, \(∠ PEG = ∠ EGR\) (Alternate angles as \(l || m\) and \(p\) is a transversal)
So, \(\frac{1}{2} ∠ PEG = \frac{1}{2} ∠ EGR\)
i.e., \(∠ FEG = ∠\)
These form a pair of alternate angles for lines \(EF\) and \(HG\) with \(EG\) as transversal and they are equal also.
So, \(EF || HG\)
Similarly, \(FG || EH\) (Considering \(∠ EGF\) and \(∠ GEH\))
Therefore, quadrilateral \(EFGH\) is a parallelogram.
Also, \(∠ PEG + ∠ GES = \)\(^°\) (Linear pair)
So, \(\frac{1}{2} ∠ PEG + \frac{1}{2} ∠ GES = \frac{1}{2} \times 180^° = 90^°\)
or \(∠ FEG + ∠ GEH = 90^°\)
or, \(∠ FEH =\) \(^°\)
So, \(EFGH\) is a parallelogram in which one angle is \(90^°\).
Therefore, \(EFGH\) is a rectangle.