
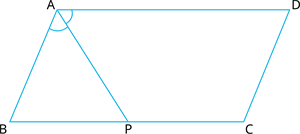
In a parallelogram \(ABCD\), where \(P\) bisects side \(BC\) and the angle \(\angle BAP\) equals \(\angle DAP\), prove that \(AD = 2CD\).
Proof:
\(ABCD\) is a parallelogram.
Therefore, \(AD∥BC\) and \(AB\) is transversal.
Therefore, \(AD∥BC\) and \(AB\) is transversal.
Then \(∠A+∠B =\) \(^°\) [sum of cointerior angles is \(^°\)]
In \(△ ABP\), \(∠PAB+∠B+∠BPA=180^°\)
\(\frac{1}{2}∠A+180°−∠A+∠BPA=180^°\) [From \(∠B=180^°−∠A\)]
\(∠BPA−\frac{∠A}{2}=0^°\)
\(∠BPA=\frac{∠A}{2}\) .....(2)
Since, \(∠BPA=∠BAP\)
\(∠BPA−\frac{∠A}{2}=0^°\)
\(∠BPA=\frac{∠A}{2}\) .....(2)
Since, \(∠BPA=∠BAP\)
\(AB=BP\) []
On multiplying both sides by \(2\), we get
\(2AB = 2BP\)
\(2AB=BC\) [As \(P\) is the mid point, ]
[since, \(ABCD\) is a parallelogram, then \(AB = CD\) and \(BC = AD\)]
Hence, proved.