
If diagonal \(AC\) of a parallelogram \(ABCD\) bisects angle \(A\),
(i) show that it also bisects angle \(C\), and
(ii) prove that \(ABCD\) is a rhombus.
(i) show that it also bisects angle \(C\), and
(ii) prove that \(ABCD\) is a rhombus.
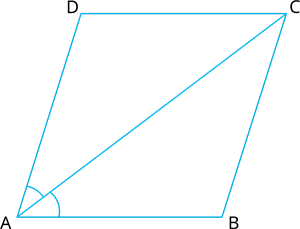
Proof:
(i) As, \(ABCD\) is a parallelogram.
\(∠BAC = ∠DCA\) ------(1) []
\(∠CAD = ∠BCA\) ------(2) []
Also, ∠CAD = ∠CAB ------(3) [\(AC\) bisects \(∠A\)]
From (1), (2) and (3), we have \(∠DCA = ∠BCA\)
Hence, \(AC\) bisects \(∠C\).
From (1), (2) and (3), we have \(∠DCA = ∠BCA\)
Hence, \(AC\) bisects \(∠C\).
(ii) In \(∆ABC\),
\(∠BAC = ∠DCA\) []
\(BC = AB\) ------(4) []
Similarly, \(AD = DC\) ……..(5)
But, \(ABCD\) is a parallelogram.
We know that opposite sides of a parallelogram is equal.
That is, \(AB = DC\) ------(6) (opposite sides of parallelogram)
From (4), (5) and (6), we have
But, \(ABCD\) is a parallelogram.
We know that opposite sides of a parallelogram is equal.
That is, \(AB = DC\) ------(6) (opposite sides of parallelogram)
From (4), (5) and (6), we have
As, \(ABCD\) is a parallelogram having all sides equal then it is a rhombus.