
In parallelogram \(ABCD\), points \(P\) and \(Q\) are taken on sides \(AB\) and \(CD\), respectively such that \(BP = DQ\). Prove that the lines \(BD\) and \(PQ\) bisect each other.
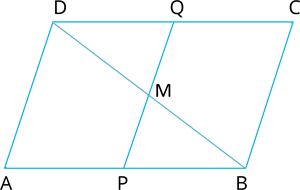
Proof:
In \(△ BMP\) and \(△ DMQ\)
\(∠MBP = ∠MDQ\) []
\(∠BMP = ∠DMQ\) []
Therefore, \(△BMP≅△DMQ\) []
Hence, \(BM = DM\) and \(PM = MQ\) []
Thus, \(BD\) and \(PQ\) bisect each other.
Hence, proved.
Hence, proved.