
Demomstrate that the diagonals of a rhombus intersect each other \(90^\circ\)
Proof:
Consider the rhombus \(ABCD\)
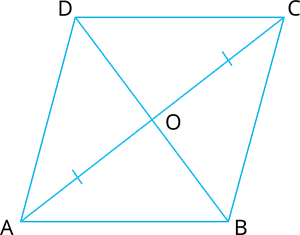
We know that \(AB = BC = CD = DA\)
Now, in \(∆ AOD\) and \(∆ COD\), \(OA =\) ( )
\(OD =\) ()
\(AD =\)
Therefore, \(∆ AOD ≅ ∆ COD\) ()
This gives, \(∠ AOD = \) (CPCT)
But, \(∠ AOD + ∠ COD =\) \(^\circ\) ()
So, \(2∠ AOD = 180^°\)
\(∠ AOD = 90^°\)
So, the diagonals of a rhombus are \(90^\circ\) to each other.
So, the diagonals of a rhombus are \(90^\circ\) to each other.
Hence proved.