
\(ABCD\) is a parallelogram where \(P\) and \(Q\) are mid-points of opposite sides of \(AB\) and \(CD\). If \(AQ\) intersects \(DP\) at \(S\) and \(BQ\) intersects \(CP\) at \(R\), then prove that \(DPBQ\) is a parallelogram.
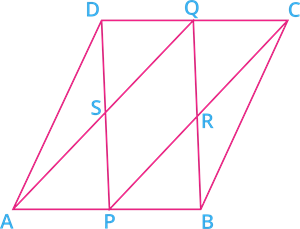
|
S. No.
|
Statement
|
Reason
|
|
1.
|
\(PB \ || \ DQ\)
|
Since
|
|
2.
|
|
\(P\) is the mid-point of \(AB\)
\(Q\) is the mid-point of \(CD\)
|
|
3.
|
\(AB = CD\)
|
|
|
4.
|
|
Half of the equal lines are equal.
|
|
5.
|
|
Using (2)
|
|
6.
|
\(DPBQ\) is a parallelogram
|
|
Hence, proved.
Answer variants:
\(AB \ || \ CD\)
Opposite sides of a parallelogram are equal
A quadrilateral is a parallelogram,
if a pair of opposite sides is equal and parallel
if a pair of opposite sides is equal and parallel
\(AB = \frac{1}{2} AB\) and \(DQ = \frac{1}{2} CD\)
\(PB \ || \ DQ\)
\(PB = \frac{1}{2} AB\) and \(DQ = \frac{1}{2} CD\)
A quadrilateral is a parallelogram,
if a pair of opposite sides is equal and perpendicular
if a pair of opposite sides is equal and perpendicular
\(AD \ || \ CB\)
All the sides of a parallelogram are equal