
Prove that the diagonals of a square are equal and bisect each other at right angles.
Let \(TUVW\) be a square.
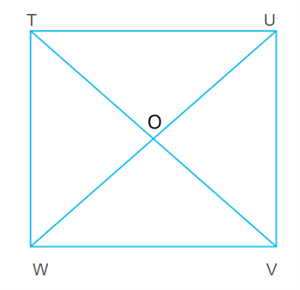
In \(∆\)\(WVU\) and \(∆\)\(TUV\),
\(WV=TU\)(sides of square are equal)
\(VU=UV\) (common)
\(∠\)\(WVU\) \(= ∠\)\(TUV\)\(=90^°\)
Therefore, by congruency, \(∆\)\(WVU\) \(≅ ∆\)\(TUV\)
So,\(WU\)\( = \)\(TV\). [By C.P.C.T.] -----(1)
Hence, the diagonals of the square are equal in length.
In \(∆\)\(WOV\) and \(∆\)\(UOT\), we have
\(∠\)\(WOV\) \(= ∠\)\(UOT\)-----[Vertically opposite angles]
\(∠\)\(WVO\)\( = ∠\) \(UTO\)-----[Alternate interior angles are equal]
\(WV\)\(= \) \(UT\)------[Sides of a square are always equal]
Therefore, by congruency, \(∆\)\(WOV\) \(≅ \) \(∆\)\(UOT\),
\(WO\)\( =\) \(UO\) \(= \)\(OV\) \(=\) \(OT\)
Hence, the diagonals of the square bisect each other ---- (2)
Now , In \(∆\)\(WOV\) and \(∆\)\(UOV\)
As we had proved that the diagonals bisect each other,
\(WO\)\( = \)\(UO\)
\(WV\)\( = \)\(UV\) [Sides of a square are equal]
\(VO\)\( = \)\(VO\) [Common]
Therefore by \(SSS\) congreuncy \(∆\) \(WOV\)\(≅ ∆\)\(UOV\)
So, \(∠\) \(WOV\)\(= ∠\) [By C.P.C.T.] -----(3)
\(∠\)\(UOV\) \(+ ∠\)\(WOV\) \(= 180^°\) (linear pair)
Now, \(2\)\(∠\) \(UOV\)\(= 180^°\) [By (3)] -----(4)
Therefore, \(UOV\)\(= 90^°\) -----(4)
From (1), (2) and (4), we get the diagonals of the square are equal and bisect each other at right angles.