
Prove that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
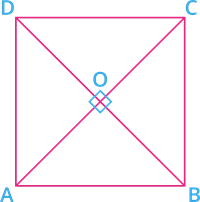
Proof: In \(\Delta AOD\) and \(\Delta COD\):
\(OA = OC\) [Given]
\(\angle AOD = \angle COD\) [Given]
\(OD = OD\) [Common side]
\(OA = OC\) [Given]
\(\angle AOD = \angle COD\) [Given]
\(OD = OD\) [Common side]
Thus, by congruence rule, \(\Delta AOD \cong \Delta COD\)
\(AD =\) [by CPCT] - - - - - (I)
Similarly, we can prove that:
\(\Delta AOD \cong \Delta BOC\), so \(AD = BC\).
\(\Delta AOD \cong \Delta AOB\), so \(AD = AB\).
\(\Delta AOD \cong \Delta BOC\), so \(AD = BC\).
\(\Delta AOD \cong \Delta AOB\), so \(AD = AB\).
Thus, \(AB = BC = CD =\) - - - - (II)
We know that, "if each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram".
Hence, \(ABCD\) is a parallelogram.
In \(\Delta BAD\) and \(\Delta ADC\):
\(AB = CD\) [From (I)]
\(BD = AC\) [Given]
\(AD = AD\) [Common side]
Hence, \(ABCD\) is a parallelogram.
In \(\Delta BAD\) and \(\Delta ADC\):
\(AB = CD\) [From (I)]
\(BD = AC\) [Given]
\(AD = AD\) [Common side]
Thus, by congruence rule, \(\Delta BAD \cong \Delta ADC\)
Corresponding parts of congruence triangles are congruent.
\(\Rightarrow \angle BAD = \angle ADC\) - - - - - (III)
Since \(ABCD\) is a parallelogram, \(AB \ || \ CD\) and \(BD\) is a transversal.
The sum of the interior angles on the same side of the transversal are supplementary.
\(\Rightarrow \angle BAD + \angle ADC = 180^\circ\)
\(\Rightarrow \angle BAD = \angle ADC\) - - - - - (III)
Since \(ABCD\) is a parallelogram, \(AB \ || \ CD\) and \(BD\) is a transversal.
The sum of the interior angles on the same side of the transversal are supplementary.
\(\Rightarrow \angle BAD + \angle ADC = 180^\circ\)
\(\Rightarrow \angle BAD + \angle\) \(= 180^\circ\) [Using equation (III)]
By simplification, we get
\(\Rightarrow \angle BAD = 90^\circ\)
Since \(ABCD\) is a parallelogram with all sides equal, it is a rhombus.
A rhombus with one right angle is a square.
Hence, \(ABCD\) is a square.
\(\Rightarrow \angle BAD = 90^\circ\)
Since \(ABCD\) is a parallelogram with all sides equal, it is a rhombus.
A rhombus with one right angle is a square.
Hence, \(ABCD\) is a square.