
\(ABC\) is a triangle right angled at \(C\). A line through the mid-point \(R\) of hypotenuse \(AB\) and parallel to \(BC\) intersects \(AC\) at \(D\).
Show that
(i) \(D\) is the mid-point of \(AC\)
(ii) \(MD ⊥ AC\)
(iii) \(CM = MA = \frac{1}{2}AB\)
Proof:
(i) To Prove: \(D\) is the mid-point of \(AC\)
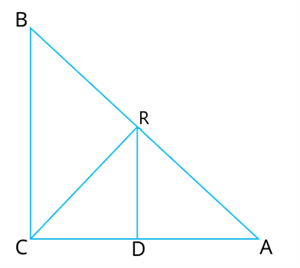
Now, from \(∆ABC\) we can see \(R\) is the mid point of side \(AB\) and
\(DR || BC\) [Given]
The by converse of Mid-point theorem, 'The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.'
Therefore, \(DC=\)
Hence, \(D\) is the mid-point of AC.
(ii) To Prove: \(RD ⊥ AC\)
Proof:
This implies, \(∠ACB = ∠ADR = ^°\)
Hence, \(RD ⊥AC\)
(iii) To Prove: \(CR = AR = \frac{1}{2}AB\).
Proof:
Considering \(∆ADR\) and \(∆CDR\)
\(AD = \) [\(D\) is the mid point of \(AC\) ]
\(∠CDR = ∠\) (\(RD ⊥AC\))
\(DR = \) ()
\(∆ADR ≅ ∆CDR\) (By )
\(CR = \) (By )
\(CR = AR= \frac{1}{2} AB\) (R is the mid point of AB)