
\(ABCD\) is a trapezium in which \(AB∥DC\). If \(E\) is the mid-point of \(AD\) and a line through \(E\) parallel to \(AB\) meets \(BC\) at \(F\). Prove that \(F\) divides \(BC\) into two equal parts.
Explanation:
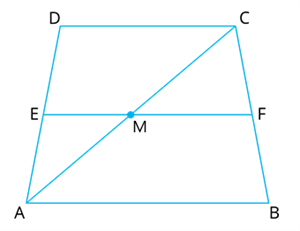
In \(△ ADC\),
is mid-point of \(AD\) and \(ME∥CD\).
By converse of mid-point theorem, 'The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.'
\(M\) is the mid point of .
In \(△ CBA\),
is mid point of \(AC\) and \(MF∥\).
By converse of mid-point theorem, 'The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.'
\(F\) is the mid-point of
Hence, \(F\) divides \(BC\) into two equal halves.
Answer variants:
F
M
E
CD
AB
AC
BC