In \(∆ ABC\), the bisector \(AD\) of \(∠ A\) is perpendicular to side \(BC\).
Show that \(AB = AC\) and \(∆ABC\) is isosceles.
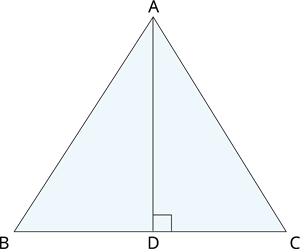
Proof:
In \(∆ABD\) and \(∆ACD\),
\(∠ BAD = ∠ \) (Given)
\(AD = AD\) (Common)
\(∠ ADB = ∠ ADC = \)\(^{o}\) (Given)
Then, by \(∆ ABD ≅ ∆ ACD\)
So, \(AB = AC\) (By CPCT)
Therefore, \(∆ ABC\) is an isosceles triangle.
Hence, we proved.