\(AB\) is a line segment and \(P\) is its mid-point. \(D\) and \(E\) are points on the same side of \(AB\) such that \(∠ BAD = ∠ ABE\) and \(∠ EPA = ∠ DPB\).
Show that:
(i) \(∆ DAP ≅ ∆ EBP\)
(ii) \(AD = BE\)
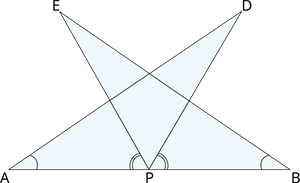
(i) Proof:
\(P\) is the mid-point of line \(AB\),
So \(AP = BP\)
Also, \(∠ BAD = ∠ ABE\) and \(∠ EPA = ∠ DPB\)
Now adding \(∠DPE\) on both the sides of two equal angle, we get:
\(∠ EPA = ∠ \)
\(∠ EPA + ∠ DPE = ∠ DPB + ∠DPE\)
Which implies that two angles \(∠ DPA = ∠ EPB\)
In \(∆ DAP\) and \(∆ EBP\),
\(∠ DPA = ∠ EPB\) [Proven] ----- (1)
\(AP = BP\) [Given] ---- (2)
\(∠ BAD = ∠ ABE\) [given] ---- (3)
Thus, by Congruence rule \(ΔDAP ≅ ΔEBP\)
Hence, we proved.
(ii) Proof:
Since \(ΔDAP ≅ ΔEBP\), then by , \(AD = BE\)
Hence, we proved.