Line \(l\) is the bisector of an angle \(∠ A\) and \(B\) is any point on \(l\). \(BP\) and \(BQ\) are perpendiculars from \(B\) to the arms of \(∠A\).
Show that:
(i) \(∆ APB ≅ ∆ AQB\)
(ii) \(BP = BQ\) or \(B\) is equidistant from the arms of \(∠A\).
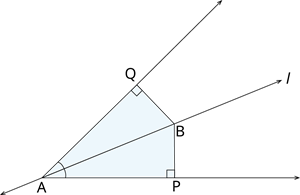
(i) Proof:
In \(ΔAPB\) and \(ΔAQB\), we have:
\(∠ APB = ∠ AQB\) [Given] ---- (1)
\(∠BAP = ∠\) [\(l\) is the bisector \(A\)] ---- (2)
\(AB=AB\) [Common side] ---- (3)
Thus, by congruence rule\(ΔAPB ≅ ΔAQB\)
Hence, we proved.
(ii) Proof:
Since \(ΔAPB ≅ ΔAQB\), then by \(BP = BQ\)
Hence, we proved.