\(ABC\) is an isosceles triangle in which altitudes \(BE\) and \(CF\) are drawn to equal sides \(AC\) and \(AB\) respectively. Show that these altitudes are equal.
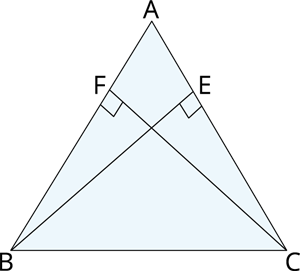
Proof:
In \(∆AEB\) and \(∆AFC\),
\(∠E = ∠\) ()
\(∠A = ∠A\) [common angle]
\(AB = \) ()
Therefore, \(∆AEB≅∆AFC\) [By Congruence Rule]
\(BE = CF\) [By \(C.P.C.T\)]
Hence, we proved.