\(ABC\) is a triangle in which altitudes \(BE\) and \(CF\) to sides \(AC\) and \(AB\) are equal.
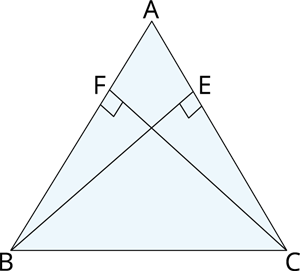
Show that
(i) \(∆ ABE ≅ ∆ ACF\)
(ii) \(AB = AC\), i.e., \(ABC\) is an isosceles triangle
Proof:
(i) In \(∆ABF\) and \(∆ACF\),
\(∠E=∠F\) []
Therefore, \(∆AEB≅∆AFC\) [By Congruence rule]
Hence, we proved.
(ii) \(AB=AC\) []
That is, \(ABC\) is an isosceles triangle.
Hence, we proved.