In the below figure, \(ABC\) is a right triangle and right angled at \(B\) such that \(\angle BCA = 2 \angle BAC\). Show that hypotenuse \(AC = 2 BC\).
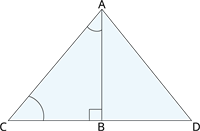
Proof:
Produce \(CB\) to a point \(D\) such that \(BC = BD\). Join \(AD\).
In \(\triangle ABC\) and \(\triangle ABD\), we have:
\(BC = BD\) [Construction]
\(AB = AB\) [Common side]
\(\angle ABC = \angle \) [Each of \(90^{\circ}\)]
Thus, by congruence rule\(\triangle ABC \cong \triangle ABD\)
Then, \(\angle CAB = \angle DAB = x\) [By CPCT] ---- (\(1\))
\(AC = \) [By CPCT] ---- (\(2\))
\(\angle CAD = \angle CAB + \angle BAD\)
\(\angle CAD = x + x = 2x\) [Using (\(1\))] ---- (\(3\))
\(\angle ACD = \angle ADB = 2x\) [Using (\(2\))] ---- (\(4\))
From equations (\(3\)) and (\(4\)), we can see that \(\triangle ACD\) is an triangle.
That is, \(AC = \)
\(\Rightarrow AC = 2BC\) [Since \(BC = BD\)]
Hence, we proved.