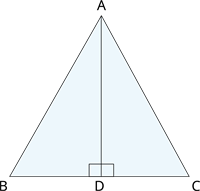
\(ABC\) is an isosceles triangle with \(AB = AC\) and \(D\) is a point on \(BC\) such that \(AD \perp BC\). To prove that \(\angle BAD = \angle CAD\), a student proceeded as follows:
In \(\triangle ABD\) and \(\triangle ACD\),
\(AB = AC\) [Given]
\(\angle B = \angle C\) [because \(AB = AC\)]
and \(\angle ADB = \angle ADC\)
Therefore, \(\triangle ABD \cong \triangle ACD\) [AAS]
So, \(\angle BAD = \angle CAD\) [CPCT]
What is the defect in the above arguments?
[Hint: Recall how \(\angle B = \angle C\) is proved when \(AB = AC\)].
Proof:
In \(\triangle ABC\),
\(AB = AC\) [Given]
We know that the angles opposite to sides are equal
\(\angle ABC = \angle ACB\) ---- (\(1\))
In \(\triangle ABD\) and \(\triangle ACD\), we have:
\(AB = AC\) [Given]
\(\angle ADB = \angle \) [Since \(AD \perp BC\)]
\(\angle ABD = \angle ACD\) [Using (\(1\))]
Thus, by congruence rule, \(\triangle ABD \cong \triangle ACD\)
So, \(\angle BAD = \angle CAD\) [By CPCT]
Therefore, the defect in the given argument is \(\angle ABD = \angle ACD\).