\(P\) is a point equidistant from two lines l and m intersecting at point \(A\). Show that the line \(AP\) bisects the angle between them.
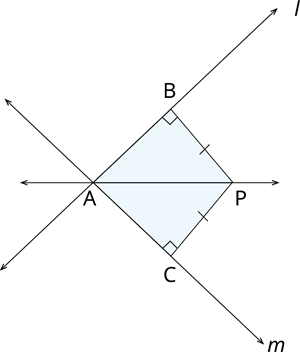
Proof:
Let us consider \(∆ PAB\) and \(∆ PAC\).
In these two triangles, \(PB = PC\) (Given)
\(∠ PBA = ∠\) \(= 90^°\) (Given)
\(PA = PA\) (Common)
So, by rule, \(∆ PAB ≅ ∆ PAC\)
So, \(∠ PAB = ∠ PAC\) (By CPCT)
Hence, we proved.