\(ABCD\) is a quadrilateral in which \(AD = BC\) and \(∠ DAB = ∠ CBA\).
Prove that:
(i) \(∆ ABD ≅ ∆ BAC\)
(ii) \(BD = AC\)
(iii) \(∠ ABD = ∠ BAC\).
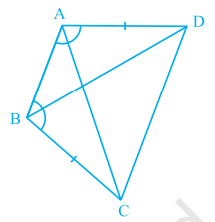
Proof:
(i) Considering two triangles \(ΔABD\) and \(ΔBAC\).
Here, \(AD =\) [Given] ----(1)
\(∠ DAB = ∠\) [Given] ---(2)
\(AB=AB\) [Common side] ---(3)
Therefore, by congruence rule\(ΔABD ≅ ΔBAC\)
Hence, we proved.
(ii) Since \(ΔABD ≅ Δ\) [By SAS Congruence rule]
So, by , \(BD = AC\)
Hence, we proved.
(iii) Since \(ΔABD ≅ ΔBAC\) [By SAS Congruence rule]
So, by \(∠ABD = ∠BAC\)
Hence, we proved.