In an isosceles triangle \(ABC\) with \(AB = AC\), \(D\) and \(E\) are points on \(BC\) such that \(BE = CD\). Show that \(AD = AE\).
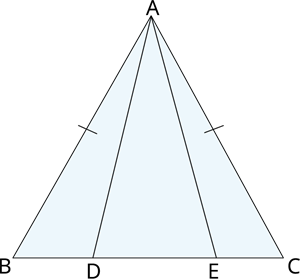
Proof :
In \(∆ ABD\) and \(∆ ACE\),
\(AB = AC\) ----(1) (Given)
\(∠ B = ∠ C\) ----(2) ()
That is, \(BD =\) ---- (3)
So, \(∆ ABD ≅ ∆ ACE\) (Using (1), (2), (3) and rule).
This gives \(AD = AE\) (By )
Hence, proved.