\(CDE\) is an equilateral triangle formed on a side \(CD\) of a square \(ABCD\). Show that \(\triangle ADE \cong \triangle BCE\).
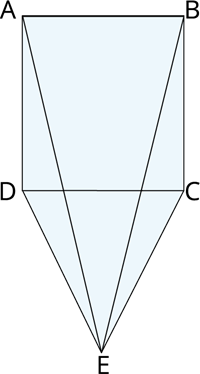
Proof:
\(\angle\)\(=\) \(\angle ADC + \angle EDC\)
\(\angle\) \(=\) \(\angle BCD + \angle ECD\)
\( =\) = \(150^{\circ}\)
\(\triangle ADE \cong \triangle BCE\) \([By Congruence rule]\)
Hence Proved