\(D\) and \(E\) are points on side \(BC\) of \(\triangle ABC\) such that \(BD = CE\) and \(AD = AE\). Show that \(\triangle ABD \cong \triangle ACE\).
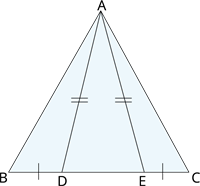
Proof:
\(\angle ADE = \angle\) ---- (\(1\)) [Angles opposite to equal sides are equal]
\(\angle\) \(=\) \(180^{\circ} - \angle ADE\)
\(\angle\)\(=\) \(180^{\circ} - \angle AED\)
\(\angle ADB = \angle\)
Thus, \(\triangle ABD \cong \triangle ACE\) [By Congruence rule]
Hence, proved.