\(l|| m\) and \(M\) is the mid-point of a line segment \(AB\). Show that \(M\) is also the mid-point of any line segment \(CD\), having its end points on \(l\) and \(m\), respectively.
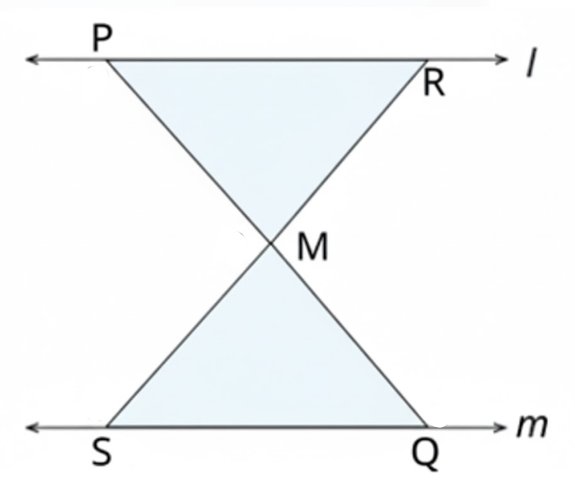
Proof:
Consider \(\Delta AMC\) and \(\Delta BMD\),
\(\angle BAC = \angle\) ()
\(AM = \) ()
\(\angle AMC = \angle \) ()
Thus, \(\Delta AMC \cong \Delta BMD\) (by congruence rule).
By CPCT, \(MC = \)
Hence, \(M\) is the midpoint of \(CD\).