Answer variants:
Angle in a semicircle is \(90^{\circ}\)
Sum of the two acute angles in a right-angled triangle is \(90^{\circ}\)
Sum of opposite angles of a cyclic quadrilateral is \(180^{\circ}\).
Angles in the same segment are equal.
The linear pair of angles are always supplementary
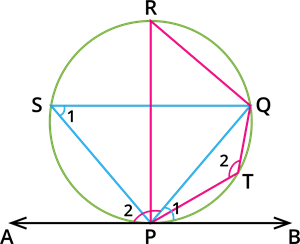
In the figure, check that the angles with equal numbers are equal.
Answer the following with suitable theorems:
|
Angles
|
Theorems
|
| \(\angle QRP\) \(=\) \(\angle PSQ\) | |
| \(\angle PSQ\) \(+\) \(\angle PTQ\) \(=\) \(180^{\circ}\) | |
| \(\angle QPA\) \(+\) \(\angle QPB\) \(=\) \(180^{\circ}\) | |
| \(\angle RQP\) \(=\) \(90^{\circ}\) | |
| \(\angle QRP\) \(+\) \(\angle RPQ\) \(=\) \(90^{\circ}\) |