A tangent to a circle is a line that touches a circle at exactly one point, called the point of tangency. If a tangent is drawn to a circle from an external point, then the square of length of tangent drawn is equal to difference of squares of distance of the tangent from the centre of circle and radius of the circle.
Based on the above information try to find the answers for the below questions.
1. If \(AB\) is a tangent to a circle with centre \(O\) at \(B\) such that \(OA = 13 \ cm\) and \(AB = 5 \ cm\), then \(OB = \)
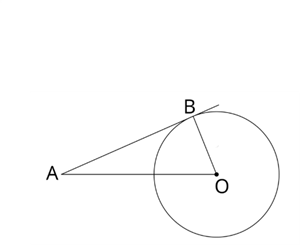
2. In the adjoining figure, radius of the circle is
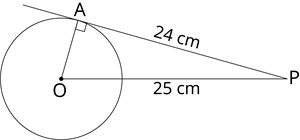
3. In the adjoining figure, length of tangent \(OA\) is
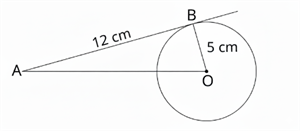
4. \(PT\) is a tangent to a circle with centre \(O\) and diameter \(40 \ cm\). If \(PT = 21 \ cm\), then \(OP = \)
