The pair of tangents \(CP\) and \(DP\) drawn from an external point \(P\) to a circle with centre \(O\) are perpendicular to each other. If so, then prove that the quadrilateral formed by the radii joining the ends of the tangents is a square.
Proof:
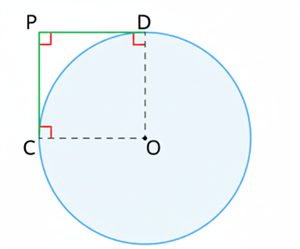
Given that, \(\angle CPD\) \(=\) \(90^{\circ}\).
By the theorem \(1\), we have:
\(OC\) \(\perp\) \(PC\) and \(OD\) \(\perp\) \(PD\).
Thus, \(\angle OCP\) \(=\) \(\angle ODP\) \(=\) \(90^{\circ}\).
We know that:
The sum of all the angles in a quadrilateral is
So, \(\angle CPD\) \(+\) \(\angle OCP\) \(+\) \(\angle ODP\) \(+\) \(\angle COD\) \(=\) \(360^{\circ}\)
\(90^{\circ}\) \(+\) \(90^{\circ}\) \(+\) \(90^{\circ}\) \(+\) \(\angle COD\) \(=\) \(360^{\circ}\)
\(270^{\circ}\) \(+\) \(\angle COD\) \(=\) \(360^{\circ}\)
\(\angle COD\) \(=\) \(360^{\circ}\) \(-\) \(270^{\circ}\)
\(\angle COD\) \(=\) \(90^{\circ}\)
By theorem \(2\), we have:
\(PC\) \(=\)
Also, \(OC\) and are equal (radius).
Here, all the four angles of the quadrilateral are equal.
Then, it is evident that all four sides are also equal.
Therefore, by the properties of the quadrilateral, we can conclude that it is a square.
Hence, proved.