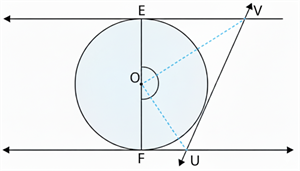
In the given figure, EF is a dimeter of the circle with centre \(O\). EV, FU and UV are tangents to the circle. Check that \( \angle UOV = 90^\circ\).
Proof:
Draw: Poin \(O\) meets UV at W.
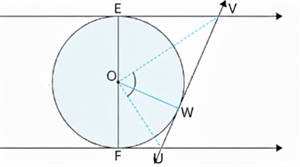
In \( \Delta \) \(OFU\) and \( \Delta\) \(OUW\),
\( FU = UW \) (Tangents from same external point)
\( OU = OU\) (Common side)
\( OF =\) (Radii)
Thus, \( \Delta OFU \cong \Delta OUW\) (by congruence).
Hence, \( \angle FOU = \angle UOW\) (by CPCT).
Similarly, \( \Delta EOV \cong \Delta WOV\)
\( \angle EOV = \angle\) (by CPCT)
Since \( EOF\) is a straight line,
\( \angle EOF =\) \(^\circ\)
\( \angle EOV + \angle VOW + \angle WOU + \angle FOU = 180^\circ\)
\( \angle VOW + \angle VOW + \angle WOU + \angle WOU = 180^\circ\)
\( 2 \angle VOW + 2 \angle WOU = 180^\circ\)
\( \angle VOW + \angle WOU = 90^\circ\)
\( \angle UOV = 90^\circ\)
Hence proved.