A circle with centre \(O\) and radius \(8 \ cm\) is inscribed in a quadrilateral \(ABCD\) in which \(P\), \(Q\), \(R\) and \(S\) are the points of contact as shown. If \(AD\) is perpendicular to \(DC\), \(BC = 31 \ cm\) and \(BS = 24 \ cm\), then find the length \(DC\).
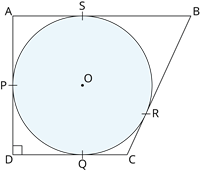

\(RC \) \(=\) \(cm\)
\(OQ\) \(=\) \(cm\)
\(OP\) \(=\) \(cm\)
Length of \(DC\) \(=\) \(cm\)