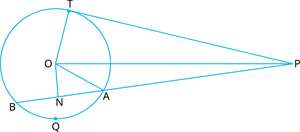
In given figure, from an external point \(P\), a tangent \(PT\) and a line segment \(PAB\) is drawn to a circle with centre \(O\). \(ON\) is perpendicular on the chord \(AB\). Check that:
(i) \(PA \cdot PB = PN^2 - AN^2\)
(ii) \(PN^2 - AN^2 = OP^2 - OT^2\)
(iii) \(PA \cdot PB = PT^2\)
Proof:
(i) \(PA \cdot PB =\) \((PN -\) \()\)\((PN + BN)\)
\(= (PN - AN)\)\((\)\(+AN)\) \((\)As \(AN = BN\) \()\)
\( =PN^2 - AN^2\)
(ii) \(PN^2 - AN^2 = (OP^2 - ON^2) - AN^2\) \((\)As \(ON \perp PN\) \()\)
\(= OP^2 -\)\((\) \(^2 + AN^2)\)
\(= OP^2 -\) \(^2\) \((\)As \(ON \perp AN\) \()\)
\(= OP^2 - OT^2\) \((\)As \(OA = OT\) \()\)
(iii) In \(\Delta \), by Pythagoras theorem,
\(OP^2 - OT^2 = PT^2\)
From (i) and (ii),
\(PA \cdot PB =\)\(^2 - OT^2\)
\(= PT^2\)
Hence proved.