From a point on a bridge across the river, the angles of depressions of the banks on opposite sides of the river are \(30^\circ\) and \(60^\circ\) respectively. If the bridge is at a height of \(4 \ m\) from the banks, find the width of the river.
Answer:
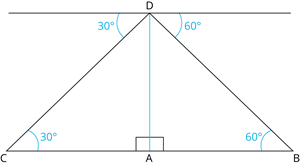
In \(\Delta ABD\),
\(\tan 60^\circ = \)
\(AB =\)\(/\sqrt{3}\)
In \(\Delta ACD\),
\(\tan 30^\circ = \)
\(AC =\)\( \sqrt{3} \ m\)
\(BC = AB + AC\)
Substituing the known values and simplifying then we get,
The width of the rive \(=\) \(m\).