A person in a helicopter flying at the height of 655 \(m\) above sea level observes two ships lying opposite to each other on the sea. The angles of depression of the ships are 45\(^{\circ}\) and 30\(^{\circ}\).Find the distance between the two ships .
(Note: Substitute \(\sqrt{3} = 1.732\) if necessary.)
Answers:
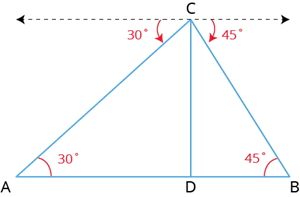
In the right \(\triangle CDA\), \(tan \ \theta =\)
\(AD=\) \(m\).
In the right \(\triangle CDB\), \(tan \ \theta =\)
\(DB=\)
Therefore, the distance between the two ships is \(m\).