A air-filled sphere shaped balloon of radius \(r\) subtends an angle of \(60^\circ\) at the eye of an observer. If the angle of elevation of its centre is \(45^\circ\) from the same point, then prove that height of the centre of the air-filled sphere shaped balloon is \(\sqrt{2}\) times its radius.
Proof:
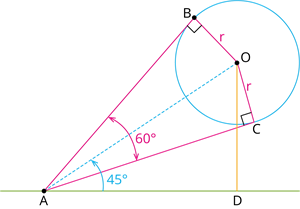
Let '\(A\)' be the observer.
\(\angle BAC = 60^\circ\) and \(\angle OAD = 45^\circ\)
Tangent at any point on the circumference of a circle makes \(90^\circ\) with the centre of the circle.
\(\angle OBA = \angle OCA =\) \(^\circ\) - - - - (1)
In \(\Delta OAB \cong \Delta OAC\),
\(\angle OBA = \angle OCA\) (by (1))
\(OA =\) ()
\(OB =\) ()
Thus, \(\Delta OBA \cong \Delta OCA\) (by RHS congruence rule).
By CPCT, \(\Delta OBA = \Delta OCA\) \(=\) \(30^\circ\)
Consider \(\Delta OAC\),
\(OA = \) - - - - (2)
Consider \(\Delta OAD\),
\(OD =\)
Hence, the height of the centre of the air-filled sphere shaped balloon is \(\sqrt{2}\) times its radius.